今回から、第2種 電気工事士の筆記試験を突破するために
『ここだけは押さえておきたい!!』というポイントについて
なるべく分かりやすいように解説していきますので
しっかり付いてきて下さいね!

学生さんから社会人まで、分かりやすくがモットーなのだ!
1.オームの法則
電気を履修している人間
電気を生業としている人間にとって
切っても切れない ハイパー当たり前知識!!
…それが、”オームの法則” です。
中学校の理科で初めて登場する、この法則。
一体何を表しているか?というと、以下の公式の通りです。
という形で表されるもので
抵抗に流れる電流の大きさで、その抵抗の両端に何ボルトの電圧が発生するか?
を表しています。
…と、言葉で書くだけじゃ意味が分からないですよね?
イメージしやすい様、実際の値を用いて説明しましょう!
例題1だと、公式に当てはめるだけで
V=2 [A] × 10 [Ω]
=20 [V]
と、簡単に導く事が出来ます。
ここでイメージが湧きにくいのは “抵抗” とか “電流” とか
目に見えない、得体のしれない存在だと思います。
これらを理解する上で、良く例に挙げられるのが “水の流れ” です。
電気は高い所から低い所へ!これ、水の流れの如し

川をイメージしてみて下さい!
川の上流は、概ね山間部であったり標高の高い場所ですね?
そこから、徐々に下流に向かって
標高の低い方へと水の流れ(=水流)は進んでいきます。
電気も同じように捉える事が出来ます。
電気の流れ(電流)も、電気的な位置(=電位)の高い場所から
低い場所へ流れる様に動きます。
この時、高い場所、低い場所の電位差を 電圧 と呼ぶわけです。
小学校の理科の実験で
乾電池、豆電球を繋いだ回路を作った経験
皆さんもお在りかと思います。
この時、豆電球の両側には
乾電池のプラス、マイナスが接続されているのですが
このプラス、マイナスに電位差があるため(乾電池なので、仮に1.5Vとしましょう)
電気は電池のプラス→マイナス方向へ流れる事になり
豆電球ピカっ!はい、やったね点灯しました! となるわけです。
ちなみに、高い場所、低い場所の電位差という言葉でイメージが湧きにくい方は
以下の様に、乾電池を垂直に立てた際
実際にプラスの方が、マイナスよりも位置的に高く
この高さ = 電圧の大きさ と見なすと分かりやすいでしょうか?

高い所から低い所へ物体が移動(=落下)するのは
地球上に存在する全ての物体に、宿命的に作用するもの!…として
イメージを頭に入れちゃいましょう!
電気の流れにくさ…それこそ、抵抗の大事な仕事!
じゃあ、抵抗って何?
そうですよね…何かイメージ湧きにくい存在です。
ただ、またしても川をイメージしてみて下さい!(好きだな)
同じ高さから流れる、2本の川があったとして
- 一方は川幅がとても広い
- そしてもう一方は、川幅がとても狭い
どちらの川の方が、より多くの水が流れるでしょうか??
イメージできますか?
はい、断然 川幅が “広い” 方が
一度に多くの水を流すことが出来ますね?
この “川幅” = “抵抗” とみなせるわけです。
要は “電流を流れにくくする” 存在そのものなのです。
ただし抵抗の両端の電圧は変化しないものとする。
先に述べた 例題1 の関係値を使ってみましょう。
例題1では、電流値=2Aと 抵抗値=10Ω が分かっている状態から
オームの法則で電圧を求めましたね?
…はい、電圧は 20Vです。
この電圧が変化しない状態で、抵抗を変えた場合に
流れる電流値を求めるには…
はい、オームの法則をちょっと変形します!!
V=IR ☞ I=V/R
電流を求めたいので、右側の形にしますと
I=20 [V] / 20 [Ω]
=1 [A]
と、導くことが出来ました!
大事なのは
『どの条件が用意されていて、どの値を求める必要があるのか?』
『どの条件を、どう扱う事で、求めたい値が導き出せるか?』
の2点だと思います。
この2点さえ抑えておけば、オームの法則に限らず
今後お話するどんな法則が出題されても大丈夫です!
仕組みを理解すれば、解けない問題はないのです。
2.合成抵抗
さて、オームの法則の基礎的な解釈を行った所で
本番の試験に頻出される“合成抵抗” の分野にメスを入れていきましょう!
…合成抵抗??笑
ですよね…何ぞや?ってお話です。。
言葉の通りですが、“合成された(と解釈された)抵抗” の事です。
公式は、以下の通り表されています。
並列部:R = RA * RB / (RA + RB)
…余計分からなくなった??汗
はい、では実際に出題されたことのある問題を使って
順番に紐解いて行きましょう!
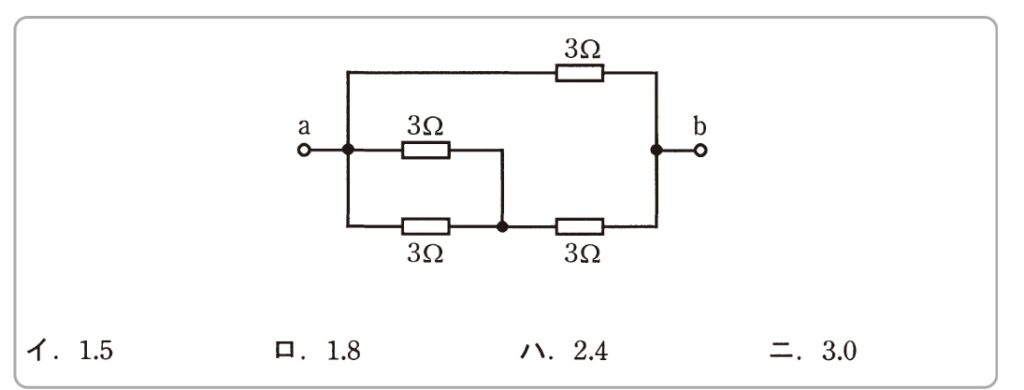
出典:平成22年度 筆記試験より
3Ωの抵抗が4個、入り乱れています…
ここで先ず
並列部分 > 直列部分
の優先順位で 考えていく事にしましょう。
理由は、“電流の流れる道を、なるべく1本に統一して考えた方が楽だから!” です。
並列部分さえ処理できてしまえば
直列部分は単純な1本の道!! 余計な寄り道をせずに済むわけです。
2-1 並列部分の理解
並列部分:図のA、及びBの抵抗について考えます。
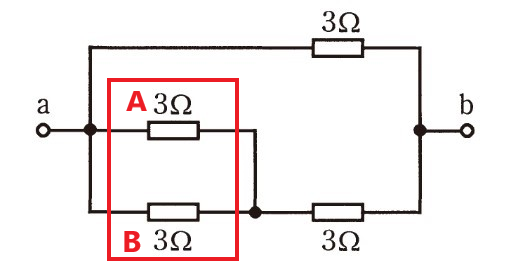
A、Bの抵抗の両端が繋がれた状態となっています。
よって、これら接続部に発生している電圧 = A、Bそれぞれの両端の電圧
は等しいという事が分かります。
要は、1本の川の流れが、途中で2本に別れて
そしてまた合流した…そんな風に捉えてもらえればOKです。
仮に、この接続部に3Vの電圧が掛かっている状態と仮定すると
それぞれの回路に流れる電流は
- 抵抗A:I = 3[V] / 3[Ω] = 1[A]
- 抵抗B:I = 3[V] / 3[Ω] = 1[A]
となり、接続部の入口→出口で、合計で 2A の電流が流れている事になります。
ここから分かるのは
A、Bの回路に流れる電流の合計 = 接続部の両端に流れる電流
という事です。
このことから、A、Bの回路を1つの回路として考えた場合
A、Bの抵抗を、1個の C という合成抵抗として見なすことができます。
抵抗Cは、オームの法則から
RC = 3[V] / 2[A]
=1.5 [Ω]
として導き出すことができます。
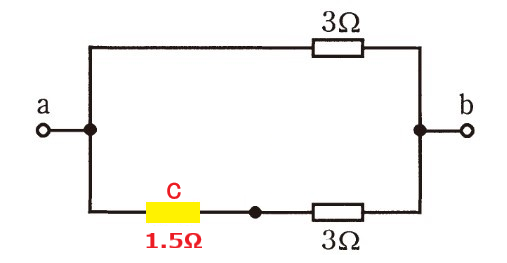
この結果から分かる事は
同じ大きさの抵抗が並列に繋がれた回路では
実際に流れる電流との関係から、抵抗値が半分の1個の抵抗と見なすことができる という事です。
どうしても公式が覚えられない!!という方は
この様に仮に電圧を掛けた場合の流れる電流から
合成抵抗を導き出す…というのも立派な解法の1つかと思います。
ちなみに、公式に当てはめると
Rc = 3 * 3 / (3 + 3)
= 9 / 6
= 1.5 [Ω]
と、秒で答えられるのですが
今大事なのは、公式よりも “何故そう考えられるのか?” という点なので御了承くださいね。
2-2 直列部分の理解
さて、並列部の合成抵抗をCとして見なせたので
次なるターゲットは、合成抵抗C、及び抵抗Dとの直列部です。
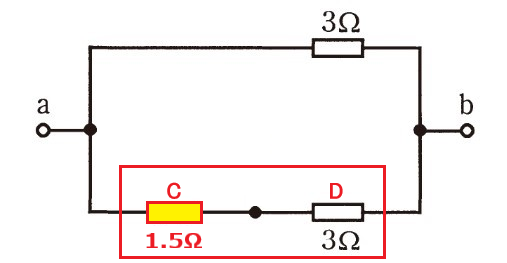
直列部分の理解は、シンプルにこうです!
“電流は不変!!”
…たった、これだけです。…えっ!?笑
何故かって? 直列部は、電流の流れる道が1つしか存在しないですから
入口→出口を伝って流れる電流の大きさは、絶対に変わりません。
鉄パイプを斜めに傾けて
高い方の穴から1個のビー玉を入れると
低い方の穴から転がり出てくるビー玉の数は??
…はい、2個なワケはないですよね? 当然1個です。
例え、途中パイプの中にゴミが溜まっていて
穴が狭くなっていようと、数は変わりません!
これと同様に
電位の高い方を入口として、一本の道を通った電流は
電位の低い出口側でも、その大きさは変化しないのです!
途中で抵抗値が変化しても…です。
この、変化しない電流が
抵抗を通過するためには、何が必要でしょうか??
…はい、オームの法則を思い出しましょう!
抵抗の両側に、電位差(=電圧:電気的な高さの差)が必要ですね?
そして、前述しましたが
“電流は、電位の高い方から低い方へ流れる!” というわけで
入口側の電位 ー 出口側の電位 = 直列部の電位差(電圧)
となり、入口と出口の間に抵抗が2個あれば
直列部の電位差は、その2個の抵抗それぞれの電位差の合計
3個になれば、3個の抵抗それぞれの電位差の合計…
という風に、シンプルに足し算していくだけでOKなのです!おめでとうございます!!
では、C、Dの直列部分に
1Aの電流を流してみましょう。
それぞれの抵抗の両端に発生する電圧は
- 抵抗C:V = 1[A] * 1.5[Ω] = 1.5[V]
- 抵抗D:V= 1[A] * 3[Ω] = 3[V]
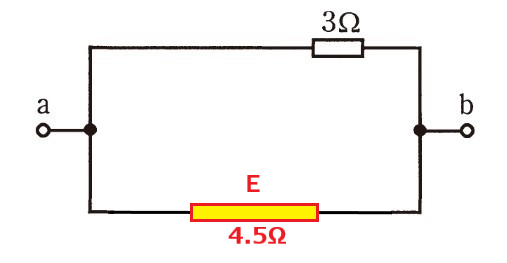
となり、C、Dを1つの抵抗 E と見なした場合の両端の電圧は
1.5V + 3V = 4.5V の電圧が掛かっていると考える事が出来ます。
C、Dは1本道であることから、まとめて考えた場合
C、Dの抵抗を、1個の E という合成抵抗として見なすことができます。
抵抗Eは、オームの法則から
RE = 4.5[V] / 1[A]
=4.5 [Ω]
として導き出すことができます。
ちなみに、公式に当てはめてみると
RE = 1.5 + 3
=4.5 [Ω]
と、単純な足し算なので
並列の時よりも数秒早く求める事が出来ます。
かなり回りくどく説明しましたが
直列部は、いたってシンプルに足し算でOK!! 忘れないでね。
2-3 答えを導いてみましょうね!
さて、残ったのは
これまで導いてきた合成抵抗 E と
a-b 間に直接接続されている抵抗 F の並列部分のみです!頑張りましょう。
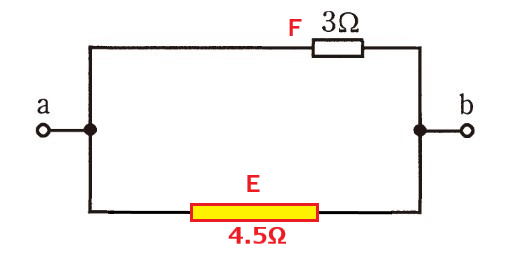
2-1 と同様、2つの回路の接続部(点a-b)両端に
9Vの電圧が掛かっている状態と仮定してみましょう!
…何故 9Vかはツッコまないで下さいね? もちろん、計算しやすいからですよ!笑
それぞれの回路に流れる電流は
- 合成抵抗 E:I = 9[V] / 4.5[Ω] = 2[A]
- 抵抗F:I = 9[V] / 3[Ω] = 3[A]
となり、接続部の入口→出口で、合計で5A の電流が流れている事になります。
E、Fの回路を1つの回路として考えた場合
⇒E、Fの抵抗を、1個の G という合成抵抗として見なした場合…でしたね?
抵抗Gは、オームの法則から
RG = 9[V] / 5[A]
=1.8 [Ω]
として導き出すことができます。
さぁ、ついにゴールしましたよ! やりました!!
本当にお疲れ様でした。
もちろん、最後の計算も
公式に当てはめると秒で計算できるわけですが
回り道して、少し理論的に考えてみたことで
理解を深めてもらうことが目的ですので、自分のモノにして頂けると非常に嬉しいです!!
理解を深めた上で、公式を覚えよう!
これ、私のモットーです!
結局、公式覚えただけでは
その物事の真理は分からないワケです。。
せっかくなら、しっかり中身を理解した上で覚えちゃいましょうね!
並列部:R = RA * RB / (RA + RB)
さて、かなり長くなってしまったので本日はここまで!!
次回は、基礎理論をどんどん実践していく回にしますので
乞うご期待くださいませ。
最後までありがとうございました。
またねー!
【本日の一言】 忘れもしない、新卒で入社した会社でのテストで
I = VR と書いたことを…。。。
訳して… ”私は仮想現実です” ハイ、5点



コメント