前回に引き続き
今回も、基礎理論編として
実際の問題を例に挙げながら
大事なポイントを押さえていこうと思います!!

まだまだ、理解しないといけない部分は沢山あるのかー?
素人にも分かりやすく教えるのだっ!!
1.頻出問題
1-1 スイッチをONしたら電圧はどうなる??
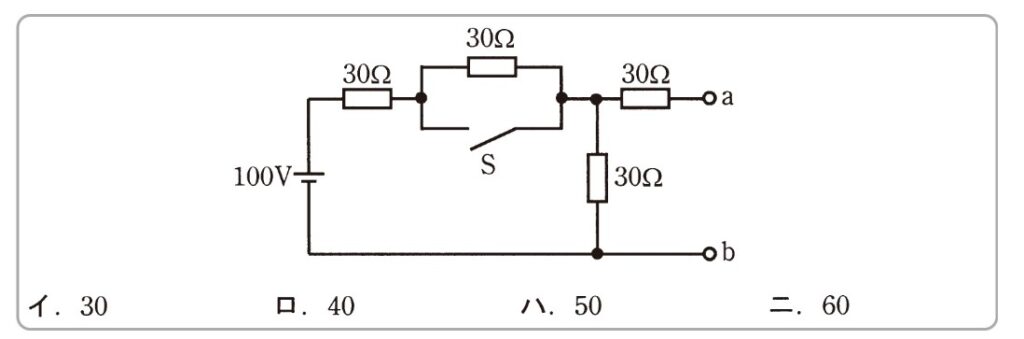
出典:平成23年度上期 筆記試験より
抵抗が盛りだくさんですね…
さぁ、どう解いて行きましょうか?
ここで重要になってくるのは
以下の2つのポイントです。
- 抵抗分圧の考え方
- 抵抗のある回路/ ない回路 が並列接続された箇所での電流の流れ方
はい、順番に解説していきましょう!
ちなみに、例題の答えは 以下にジャンプ!!↓↓↓
Point 1 抵抗分圧の解釈
電源から抵抗を通じて流れる電流のイメージを付きやすくするため
問題の図を、以下の様に置き換えて考えてみましょう。
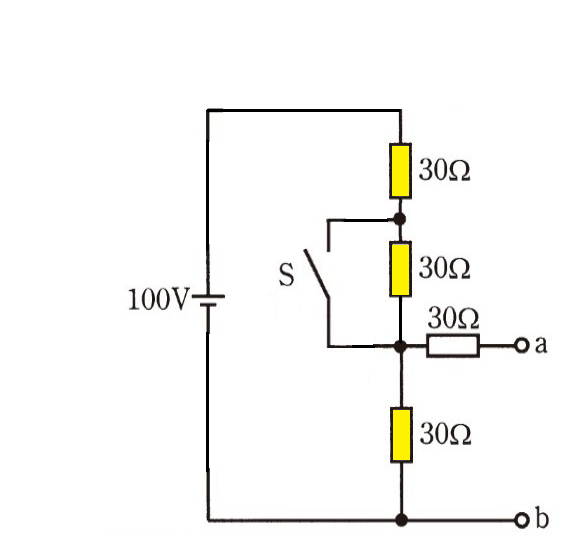
配置は変わりましたが
電源と、接続されている抵抗の関係性は変わっていません。
ここで、図の状態で電流が流れる回路を赤く着色してみます。
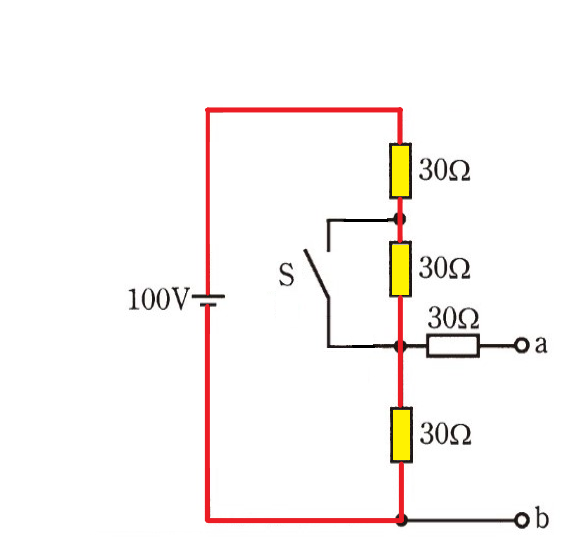
こうすると
- スイッチ部
- 端子 a へ繋がっている 30Ω抵抗
- 端子 bへ繋がる部分
に対しては、回路が途中で切れているため電流が流れない事が分かります。
よって、この状態の時は
電源 100V と 30Ω抵抗 × 3個の直列回路が電気的に接続されている
と解釈することが出来ます。
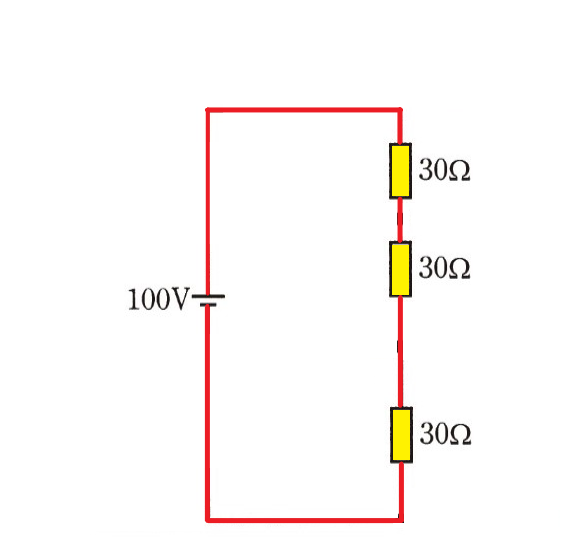
この回路に流れる電流は
前回の授業で説明した、2つの公式で導き出すことが出来ますよ!?
覚えてますか??
はい、そうです。
- オームの法則
- 合成抵抗(直列部)
でしたね?
※忘れてしまった方は、前回の授業を復習しましょう!!
↓↓↓↓↓
まず、直列部の合成抵抗 = 単純な足し算でしたね?
よって、30 [Ω] + 30 [Ω] + 30 [Ω] = 90 [Ω]
この合成抵抗 に流れる電流は、オームの法則より
I = 100 [V] / 90 [Ω] = 1.11… [A] となります。
※上の公式は、V = IR を “I” を求める形に変形したものです。
回路に流れる電流が分かった所で
合成抵抗を、一旦 最初の3個に戻してみます。
この時、それぞれの抵抗を電流が通過するために必要な電圧は??
はい、そうです! またオームの法則です。 大活躍ですね?
1個の30Ω抵抗 両端に必要な電圧 V = 1.11[A] * 30 [Ω]
= 33.3 [V] となります。
回りくどいですが、これもしっかり理解するため! 忍耐忍耐です!!
1個の抵抗の両端に 33.3 V の電圧が掛かり、同じ抵抗3個が直列に繫がっているので
33.3V * 3個 ≒ 100V になる訳です。検算もOKですね。
…さて、何かに気付きませんか??
そう、抵抗値が同じ抵抗には 等しく同じ電圧が掛かっています。
今回は、抵抗値の同じ抵抗が3個 繋がっているので
先ほどの検算の逆で、100 [V] / 3 = 33.3 [V] となり
丁度、電源電圧を 3等分している事が分かると思います。
この作用を、“抵抗分圧” と呼びます。
公式は以下の通り。
今回の例だと、3個全ての抵抗値が 30Ω なので
1個の抵抗の両端に掛かる電圧 = 100 [V] * ( 30 [Ω] / 90 [Ω])
=33.3 [V] となります。
回りくどく書きましたが
要は “同じ抵抗が3個 ⇒ 電圧は 1/3 ずつに分けましょうね!” なだけなのです!
Point2 スイッチと抵抗の並列回路 の解釈
図を元に戻して
スイッチ S と、抵抗 30Ω が並列接続されている 赤枠部に注目してみましょう。
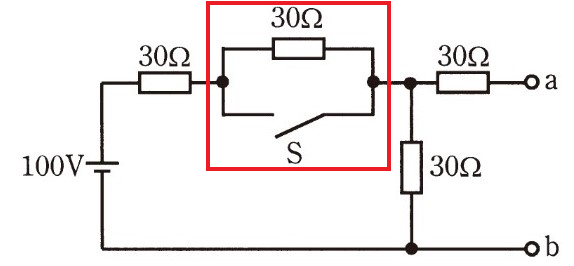
今、このスイッチ SをONにします。
すると、この赤枠部分の電流の流れはどうなるでしょうか??
うーん、これは難しいですね。。。
スイッチというものは、電気的に切り離された2点を繋ぐ役割を果たします。
身近な所で言うと、ご家庭の照明をつけたり・消したりする、アレです。
Point1 の時に、スイッチ部の回路は繋がっていないので電流は全く流れない…
ということで除外したのが、まさにスイッチの仕組みなのです。
では、スイッチ部の回路が繋がった時、赤枠部分で何が起こると思います?
まず、合成抵抗を考えてみましょう。
ここは並列部なので、30Ωの抵抗と、スイッチの抵抗…
…あれ、ちょっと待って?スイッチの抵抗値は??
…そう、書いてませんよね?? つまり、スイッチは抵抗値 “0Ω” なんです。
※厳密には 全く”0″ というわけではなく、無視できるレベルに小さい…という意味です。
便宜上、抵抗値を 0Ω として説明していきます。
では、この部分の合成抵抗は?というと、以下の公式で求めるんでしたね?
RA:30Ω抵抗 RB:0Ω スイッチとしてあてはめると
R = 30 * 0 / (30 + 0)
= 0 [Ω] という事で、赤枠部は0Ω(=ただの電路)として見なすことが出来るのです。
理屈で考えると
抵抗値が大きいということは、それだけ電流が流れにくい
…言い換えると
抵抗値が小さい(ほぼ 0)の時は、それだけ電流が流れやすいのです。
これは、オームの法則を用いて考えてみると明白で
I = V / 0[Ω] = ∞(無限大) [A]
つまり、いくらでも流れてしまいますよね?
この状態は電源のプラスとマイナスの間を抵抗負荷なしで直接つないだ状態
と同じと捉えられますよね?…所謂、ショート(短絡)です。
そんな危険な回路、一般家庭のスイッチ回路に存在してたら至るところで毎日大事故です!
そこで、全く逆の発想でオームの法則を使ってみます。
V = I * 0[Ω] = 0 [V]
そう、これが正解です!
電流の大小に依存せず、スイッチ部(抵抗値 0Ω) の両端電圧は 0V となるのです。
この事実より、スイッチと並列に接続されている 30Ω抵抗の両端電圧も 0V とみなせるため
抵抗側には電流が流れず、全ての電流がスイッチ側を通る…と見なすことができるのです!
このことから
赤枠部分は 理論的に省略が可能!という結論に至る事が出来ます。(下図)
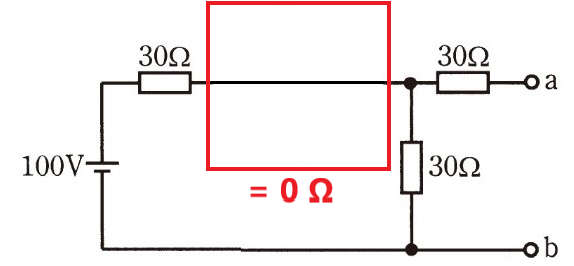
さぁ、解いてしまいましょう!
これまでの理解から
例題の回路は、以下の様に解釈できます。
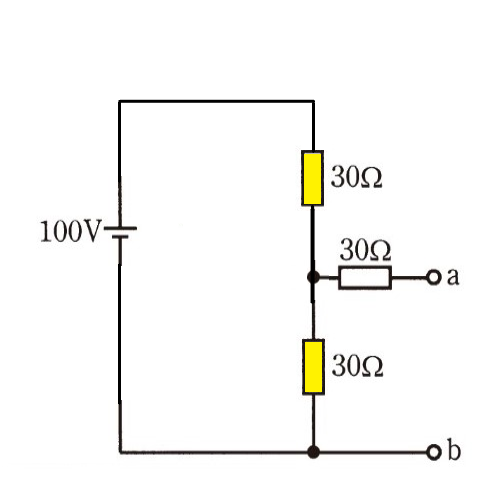
とてもシンプルになりましたね?
この形になれば、あとはPoint 1抵抗分圧を駆使するだけです!
電源に対して、30Ω抵抗が2個直列接続されている状態ですね?(図中、黄色抵抗×2)
求める電圧は、a-b間の電圧なので
黄色の抵抗のうち、下側の抵抗の両端電圧を求める事になります。
公式から
V = 100 [V] * ( 30 [Ω] / 60 [Ω])
= 50 [V] と導き出すことが出来ました。
ここで、端子a に接続されている 30Ω抵抗(白)に関しては
電源との直列回路に含まれていないため
抵抗分圧の要素としてはカウントされない点に注意です!
1-2 抵抗とインダクタンス(コイル) の回路
~編集中~




コメント