どもっ!かなとです。
世の中の電気・制御エンジニア
特に、未経験者・初心者に向け
分かる喜びと、戦う武器を与えるために情報を発信し続ける
“初学の味方” の私がやって来ました!!

今回は、プログラミングに特化したお話。。
PLCのプログラミングに関しては
“こうなった時には、こう動く“
という考え方が非常に重要です…
世の中の事象のすべては
この “シーケンス(順序動作・条件動作)” の概念で
凡そ言い表すことが出来ます。

“太陽の動き” = 東から昇り、西へ沈む
“車の操作” = アクセル踏めば進み、ブレーキ踏むと止まる
“妻”の機嫌= 誕生日を忘れると、半沢直樹化する。。
…はぁっ、恐ろしいっ!!涙
奥様の誕生日は
是非、手料理ふるまってあげてください!
(冗談です。)

言葉では、色々なパターンで表せるのですが
これを”プログラミング” に置き換えるとすると
一体、どうしたらいいのでしょう??
この考え方こそ
今回説明する
“論理回路” そのものなのです!

あぁー、また難しい単語が出てきたぞ…涙
だからワケが分からなくなって
途中で投げ出したくなるんやー!!きぃーーーー
と、数々の戦死者を生み出してきた
この論理回路なのですが
おめでとうございます!!

この記事を読むことで
“確実に” この論理回路が
理解できてしまうんです!
更には
論理回路を利用した
PLCプログラミングの考え方まで
しっかりマスターできてしまうのです!
たったの “3章” 仕立て!!
3章読み終わった時点で
もう論理回路はあなたのもの!
ラダーでどう書いていけばいいかも完璧に分かります!
差を付けたいならば
先を急ぐべしっ!!
※※かなとのPLC講座 ※※ (前回はこちら)
俺の宿敵っ!! 論理回路
既に、論理回路を
敵と認識されているあなた…

気持ちは分かりますが
先ずは、落ち着いて
論理回路って何なのか?
について、見ていきましょう!!
論理回路…
何か、”ろんり” なのか ”りんり” なのか
一瞬分かんなくなってしまいますよね。。
なので、私自身は
良く”ロジック回路” という風に呼んでます。
論理を英語にしただけですがね…
どちらで呼んでもOKです!
※”りんり” じゃないですよ? ”ろんり” です!
で、そんな論理回路が何かというと

と、検索1位のサイトで説明されています…。。
…はい、撃沈です。。涙
意味不明な単語の羅列を読んで
理解出来たら苦労しませんよね。。
そこで、私はこう説明します!

だいぶ簡略化されたでしょ?
じゃあ、どういう意味か…
例を挙げてみましょう!
あなたは、出かけるときに
靴を履きますよね?
履いてない方、是非履いてください!笑
では、玄関に行って
靴を見てみましょう。

はい、右足、左足
左右セットの一足の靴が並んでいますよね?
この状態であれば
あなたは、その”一足” の靴を履いて
お出かけすることが出来ます!

…あれっ?そこのあなた
靴が右足しかない?左足はどこ?
犬が持って行っちゃった??
あぁ、これじゃお出かけ出来ないですね。。
はい、ここで論理回路の考え方に戻ります!
右足、左足、どちらも揃っている状態
これはつまり、“一足” の靴と呼べます。
ですが、左足が見当たらない靴は
そのままでは履いて歩けないので
“一足” とは呼べませんよね?
…そう、条件が揃って導き出される結果は
その場にある靴が、”一足” であるかどうか…という
判断結果となります。
ですが、このお話には
実はもう一つの側面があります。
私は今
何という説明をしましたか??

…はい、その通り!
左右どちらも揃っている “靴” と
左足が見当たらない ”靴”
どちらも、”靴” なんです!
同じ説明をしているにも関わらず
結果が2種類存在するのは何故か??
これこそが
論理回路の結果を導くためのルールの存在です。
出ました!! 強敵 ド・モルガン!!笑
中学数学の授業で
“ド・モルガンの法則” というものを習います。

私と同年代の皆さん!
覚えていますか??
否、記憶の彼方に
Fly awayされてしまっている方も多いでしょう。。笑
数学だって言ってるのに
何やら怪しげな〇を2つ重ねて
A∩B とか意味不明な記号を羅列させられて
覚えさせられた、アレです。
そりゃ、嫌いになりますよ。。
数字、出てこないんですから…
意味が分かんないですよね?
それを習う目的を伝えずに
ただ、決められた要項として教えるという行為は
圧倒的な学習離脱者を生むという事実を
教育者はシッカリ理解して頂きたい所です。。

…話が逸れましたが。。
皆さん、”ド・モルガン” という言葉のインパクトだけ
覚えている事かと思われますが
実は、このモルガンさん
本当に素晴らしい法則なんです!!
そう、この法則こそ
論理回路の仕組みを明確に表しているのです。
じゃ、噂の2つの円に登場してもらいましょう。
Aという条件
そして、Bという条件
2つの条件が存在する時に
その判断結果がどう表されるか?
これを示すのが、2つの円の
“塗りつぶされている領域” です。
ちなみに、条件が成立している時
その条件を示す円が塗りつぶされます!
では、先ほど例に挙げた
“靴の話” を当てはめてみましょう!
A、Bの2つの条件で
先ずは、“一足” の靴が成立する条件を見てみます。
この時、条件としては
- A…左足の靴
- B…右足の靴
を当てはめることが出来ます。
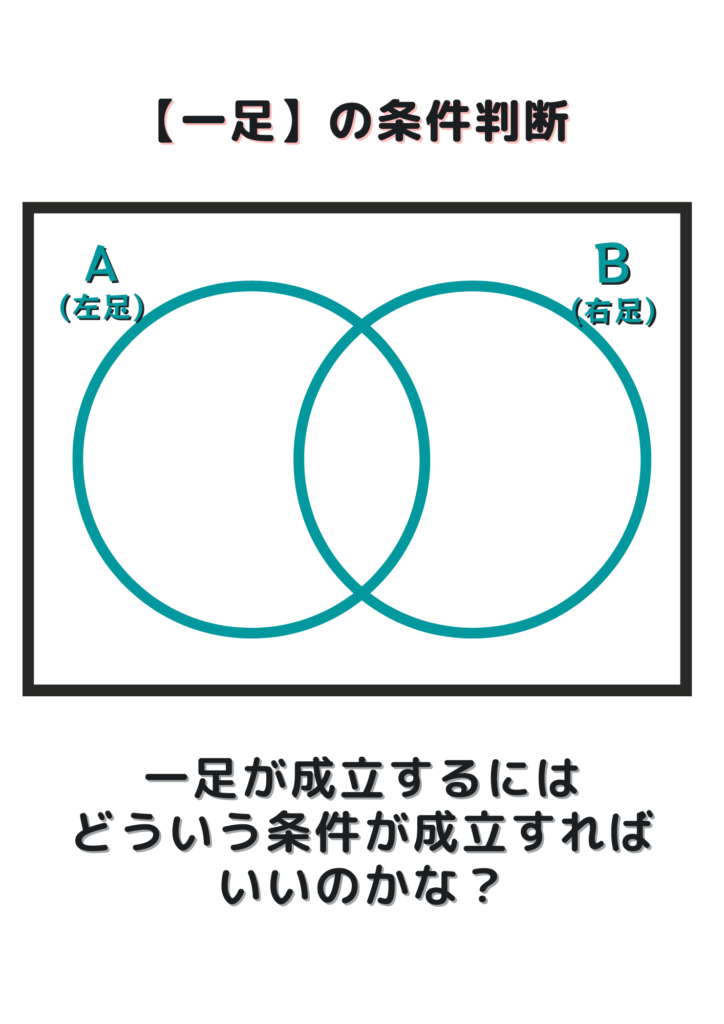
では、”一足” の靴として成立させるには
条件A、Bがどういう状態であればいいでしょう?
分かりますか??
はい、そうです。
- A(右足の靴)☞ “存在する“
- B(左足の靴)☞ “存在する“
両方とも存在していて
初めて、”一足の靴” になるんでしたね!
この時、円の図は
Aが存在している
そして、Bが存在している
つまり、AとBが重なっている
下図の領域を表していることになります。
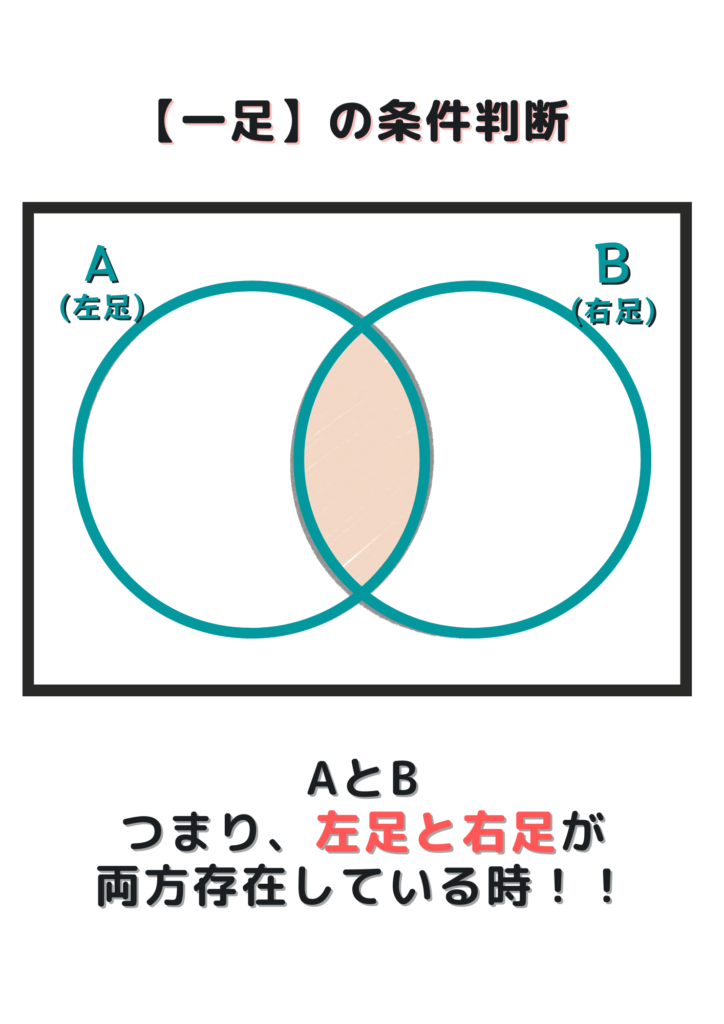
この領域の事を “論理積” と呼び
A ∩ Bという記号で表します。
(読み方は “A かつ B”)
ここは、A、Bのどちらも成立していないと
成立しない領域です。
何故、論理 “積” と呼ぶかというと
プログラム的に、これらの条件A、Bは
- 成立していない時 ☞ “0”
- 成立している時 ☞ “1”
というデジタル信号で扱います。
これらを掛け合わせた時に
どちらかが “成立していない = 0” の場合
結果はどうなるでしょう??
積 … つまり、“掛け算” の答えとなるので
1 × 0 = 0 となりますよね?
…そう、どちらかが “0” であれば
答えは必ず “0 (成立しない) ” になるのです!
だから、論理 ”積” と呼ぶんですね。
今回の例では
右足、あるいは左足のどちらかが存在しない場合は
“一足” として存在できない…
という判断結果となります。
では、“靴” の判断はどう表せるでしょう?

…勘の良い方なら
既にお気付きの事かと思いますが
右足、あるいは左足の”どちらかが” 存在する場合
これが成立条件となります。
2つの円で表すと、以下の領域となります。
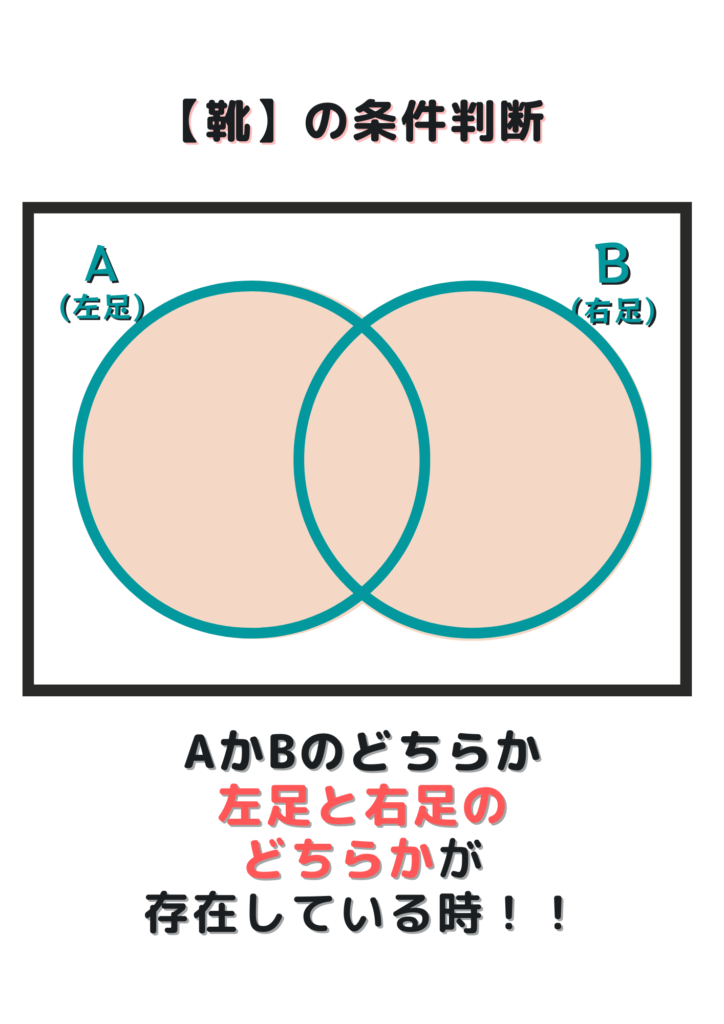
つまり、AとBで支配されている
下図の領域を表していることになります。
この領域の事を “論理和” と呼び
A ∪ Bという記号で表します。
(読み方は “A また B”)
ここは、A、Bのどちらかが成立していれば
成立するという領域です。
何故、論理 “和” と呼ぶかというと…
先ほどの 論理積とは正反対に
- 成立していない時 ☞ “0”
- 成立している時 ☞ “1”
というデジタル信号で考えた場合
これらを足し合わせた時に
どちらかが “成立していない = 0” の場合でも
和 … つまり、“足し算” の答えとなるので
1 + 0 = 1 となりますよね?
…そう、どちらかが “0” であっても
答えは必ず “1 (成立する) ” になるのです!
“靴” という結果が導かれるのは
- 右足の靴だけ存在している
- 左足の靴だけ存在している
- 右足/左足の両方とも存在している
というパターンの時です。
…あれ?
論理積でも、論理和でも
両方の条件が成立していれば
どちらも結果は成立になるの?

そう、いいポイントに気付きましたね!
2つの条件を判断するルールが異なっていても
条件が両方とも成立している場合は
問答無用で結果は “成立する” になります。
それは、2つの円の領域を見れば明らかですよね?
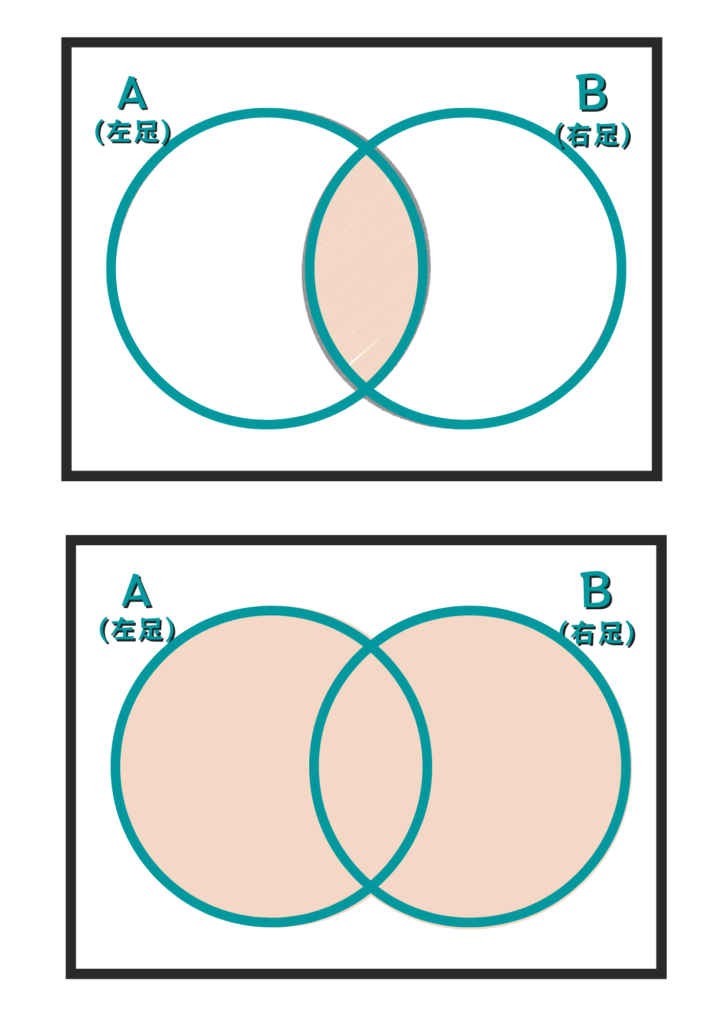
A、Bの両方とも成立する範囲…
そう、2つの円が重なり合っている領域です。
論理積、論理和共に共通の領域
つまり、成立する条件が同じなのです。
(A = 成立している / B = 成立している)
実は、この使い分けこそ
PLCプログラムでは
非常に重要な考え方になってくるのです!!
今回は
“論理積” 、”論理和” の概念の説明だけでしたが
これら
“論理積” 、”論理和” という判断条件の違いによって
求められる結果が変わってくる…
そして、
この事実を押さえておけば
論理回路というものが何なのか?
その基礎を押さえられたといっても
過言ではありません!
おめでとうございます♪
【注意】他にも、排他的論理和 など
条件は様々ありますが
今回は最もイメージしやすい内容のみ記載しています。
需要があれば、他の条件に付いても記載していきますね!
何故、論理回路を理解すれば良いの?
今、説明してきた論理回路
考え方は理解できたでしょうか?
判定するための条件が、どんな状態か?
その状態を見て、判断結果はどうなるか?
この説明を、形にしたものが
論理回路の概念です。
では、何故こんなにも”論理回路”について
理解しておくべき!と話しているのか??

それは、過去の偉大なる先人達の言葉も
去ることながら
僕自身がそれを身をもって経験したからなんです。
私自身は、新卒で
“電子回路” 設計に携わっていたのですが
大学で電気を勉強していたわけでもなく
全くの素人から飛び込んだこの業界…
そんな中、初めて
自らの中で、”分かった!!完璧にイメージできた!!“
と自信を持てたのが
この論理回路(デジタル回路)でした。

“こういう信号が入力された場合の
出力信号は、こうなる!“
当時の自分は
東芝のデジタルICを使って
様々なデジタル回路を設計していたので
ICのデータシートを毎日何時間も見ながら
回路設計を行っていました。
つまり
“こうなれば、結果はこうなる!“
“じゃあ、条件を変えれば、結果も変わってくるはず…”
という感じでロジックを整理する事を繰り返すうちに
”論理回路を理解してしまえば
様々な動作原理を言い表せるのでは??”
という心理に辿り着いたのです。
そして、ある日
見たこともない機器を渡され
“ロジックが分かってきたみたいやし
ちょっとこの仕事やってみる?“
と、上司に声掛けしてもらいました。
その機器こそ
私の人生を大きく変えることとなる
PLCだったのですが

今でも忘れません…
“この、良く分からない
線で繋がれた回路…これは、何??” 笑
ただ、そんな疑問は
やり始めて一気に消し飛びました!
論理回路、この考え方こそが
ラダーを考える上で非常に重要なのだと
一瞬で気付いたからです。
ラダーが何を表しているか
ご存知ですか??

これが、実は
“リレーのON/OFF” を示しているんです。
そう、前回の記事でもお話しした通り
“リレーシーケンスを簡略化したもの“
つまり、プログラム化したものが
ラダーの概念なのです。
そして、このリレーシーケンスこそ
論理回路を分かりやすく形にしたものなので
制御系エンジニアの方々が

リレーの組み合わせをイメージ出来ないと
動きなんて分かんないぞ!!
と口うるさく話している真の理由は
この論理回路を知っていれば
リレーシーケンスも、ラダーも
バッチリ当てはめることができるからなのです。
“やっておいて、損はない!“
どころではありません…
“やっておかないと、分かんないよ?“
と、僕はお伝えしておきます。
(脅しではないですよ?汗)
ただ、ここまで読んで下さったあなたは
論理回路が何たるか?
そこが段々とイメージ出来てきたのではないでしょうか?
大丈夫です!!
それだけでも
あなたにはセンスがあります!!
さ、では実際には
その論理回路を用いて
どうプログラミングしていくのか?
それについて見ていきましょう!!
ラダーでの論理回路の表し方は?
図を見てみましょう!
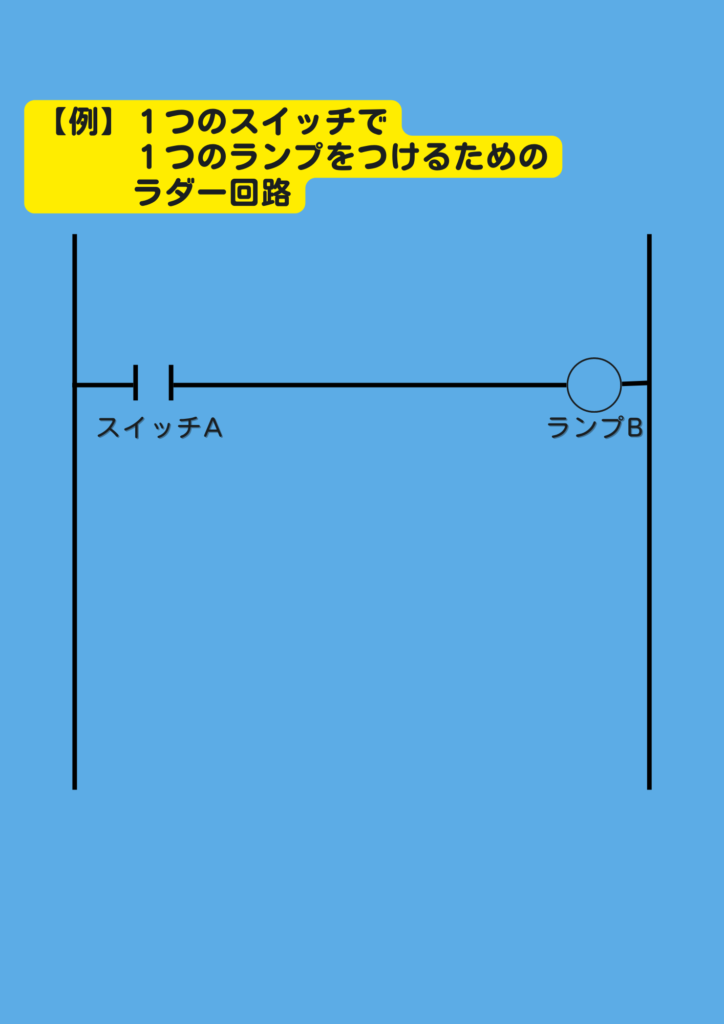
この例では
“Aというスイッチを押すことで
Bというランプが点灯する”
という論理回路をラダーで示したものです。
この時
ランプBがONする条件は
“AのスイッチをONすること”
となります。
つまり、下の図の通り
AのスイッチがONした場合です!
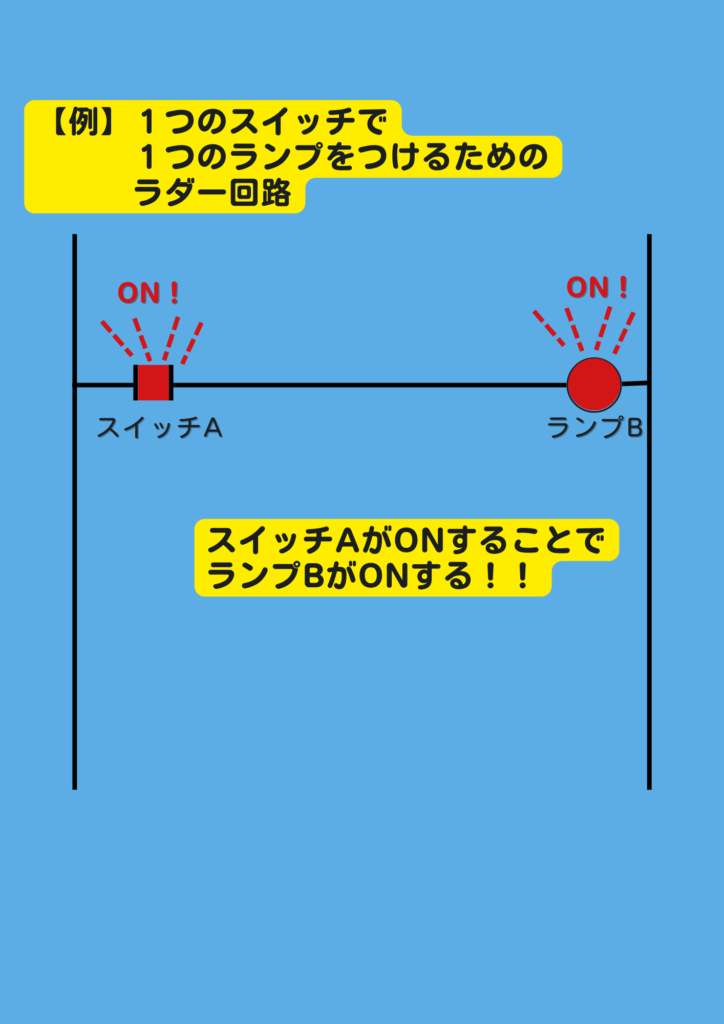
この論理回路であれば
凡そ理解できるのではないでしょうか?
AがONならばBもON…
つまり
“A = B” という式で表すことが出来ます!
シンプルですね。
ラダーでは
左右の縦に引かれている線を “母線” と呼び
左側の母線 ☞ 右側の母線に対して
電気が流れている…とイメージしてください。
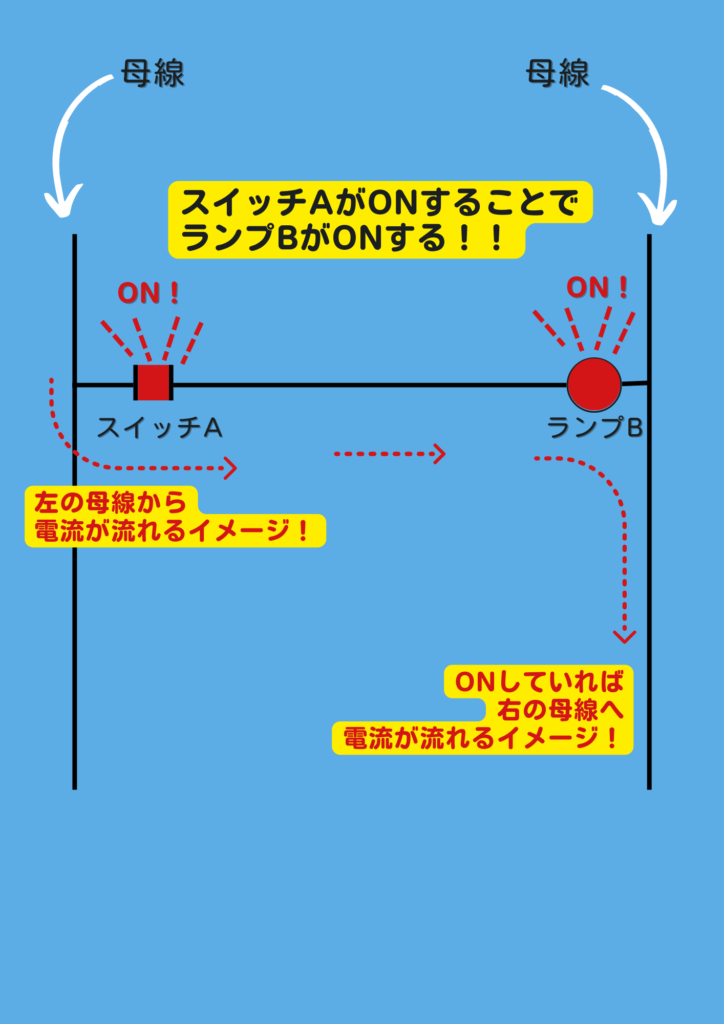
つまり、左側に書かれている条件
(今回の場合は、Aのスイッチ)
これがONすることで
ランプBに電流が流れて点灯する!
こういうイメージができます。
この時、ランプBを
“出力コイル“、あるいは “コイルOUT“
と呼びます。
いわゆる、出力信号ですね。
ラダーの基本は
“出力コイルを、どういう条件でONさせるか“
が全てです。
この概念さえ押さえておけば
あなたは今日から、ラダープログラミング可能です!
おめでとうございます♪
=====================
では、今日説明してきた
靴の例をラダーで表してみます。
先ずは、”一足” が成立する条件を
ラダーで示してみます。
それが、以下の図です。
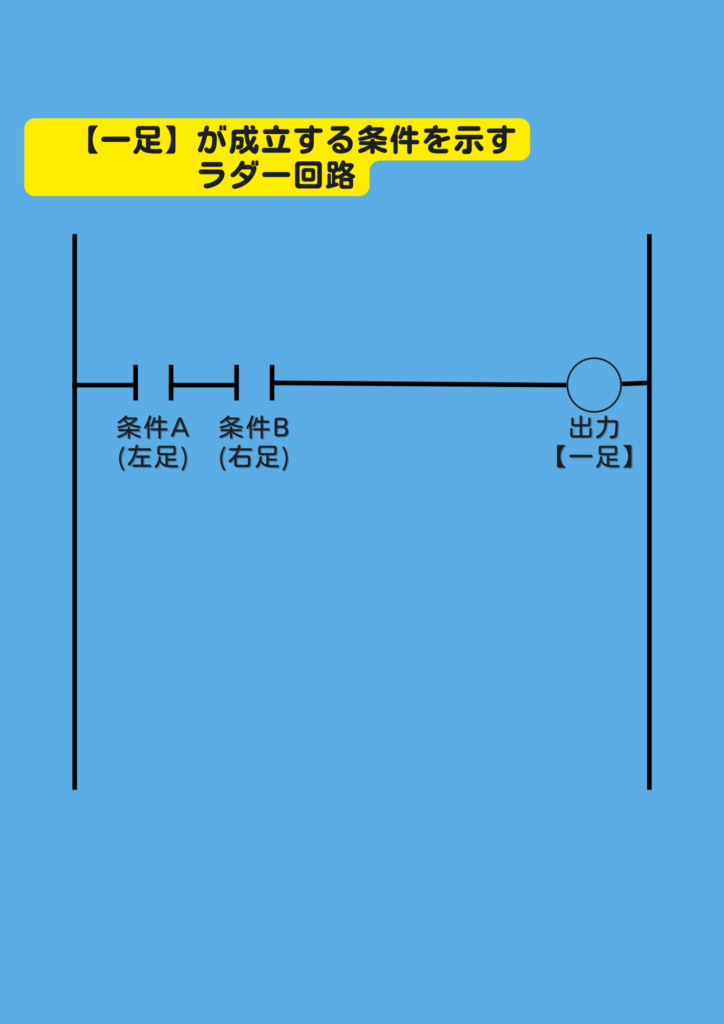
このラダーの出力コイルは
“一足” となります。
ですので、一足を成立させるための条件は
“左足”、及び “右足” の靴が
どちらも揃っている… という状態です。
今回のラダーでは
右足、左足のどちらかが成立していなければ
出力コイル “一足” はONしません。
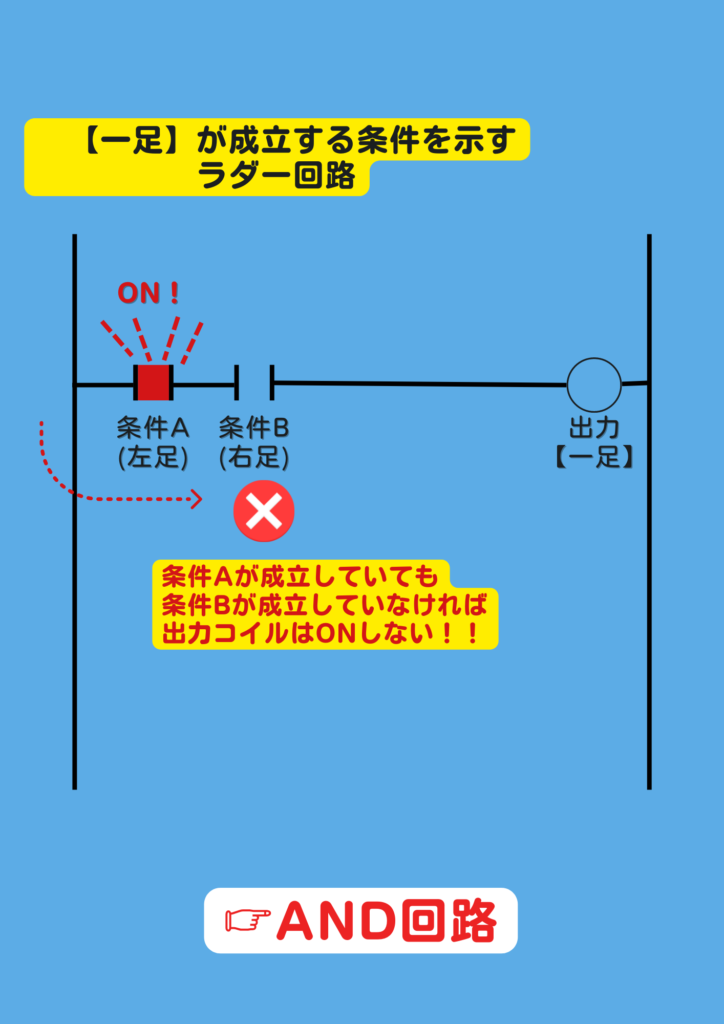
つまり、これが
“論理積” の回路をラダーで表したものとなります。
ラダーでは、この回路のことを
“AND回路” と呼びます。
AND回路は、デジタル回路でも多用される回路で
どちらの条件も成立していないと
出力は成立しない…という回路を指します。
これを、ラダーで表すと
条件が直列に接続されている…
つまり、どちらの条件も成立(ON)していないと
出力コイルに電流が流れない…
そういう回路を指します。
では、反対に
“靴” が成立する条件を
ラダーで示してみます。
それが、以下の図です。
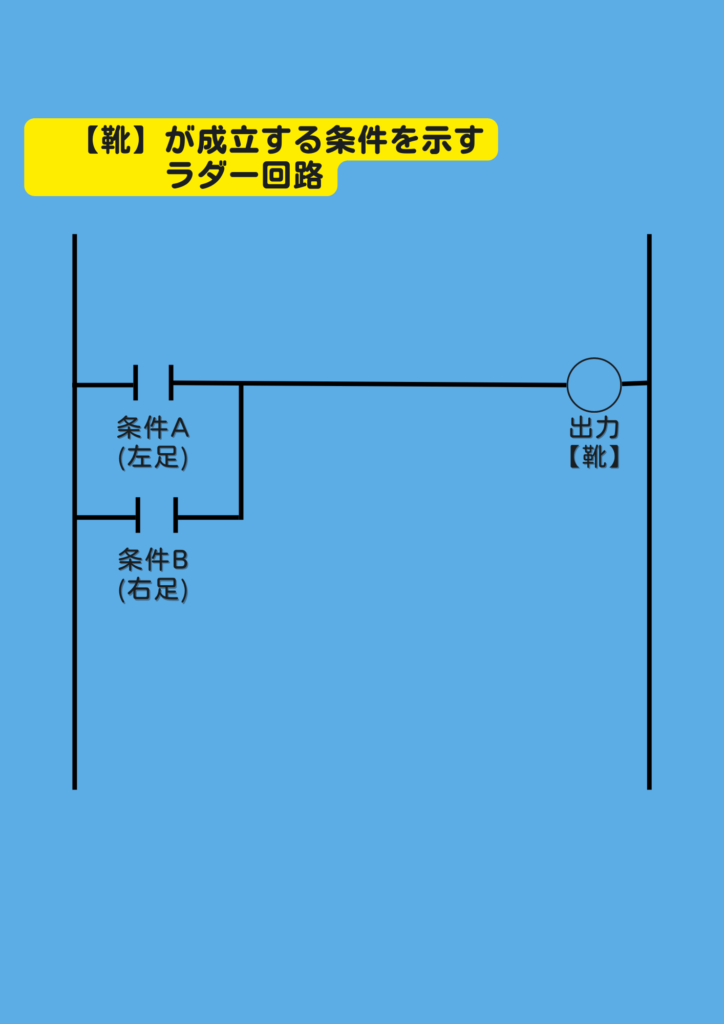
このラダーの出力コイルは
“靴” となります。
ですので、靴を成立させるための条件は
“左足”、あるいは “右足” の靴
どちらか1つが揃っている… という状態です。
今回のラダーでは
左足、右足のどちらかが成立していれば
出力コイル “靴” がONします。
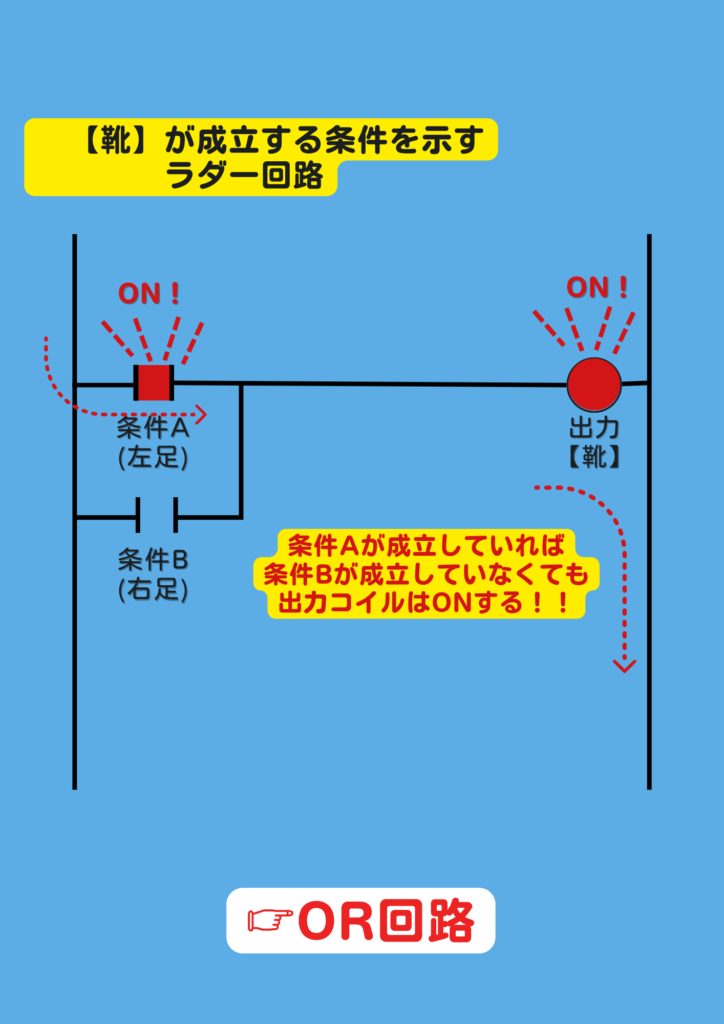
つまり、これが
“論理和” の回路をラダーで表したものとなります。
ラダーでは、この回路のことを
“OR回路” と呼びます。
OR回路も、AND回路と同様
デジタル回路で多用される回路で
どちらかの条件が成立していれば
出力は成立する…という回路を指します。
これを、ラダーで表すと
条件が並列に接続されている…
つまり、どちらかの条件が成立(ON)していれば
出力コイルに電流が流れる…
そういう回路を指します。
この2種類の論理回路の使い分け
これこそが、ラダープログラミングを行う上で
最も基本的な考え方となります。
例えば、A、B2つのスイッチがあって
出力コイルに “モータ” が設定されているとします。
例えば、この2つのスイッチを
- どちらのスイッチも押されている時に、モータを動かしたい!
- どちらかのスイッチが押された場合、モータを動かしたい!
この2つの条件は
全く持って異なる性質を持っています。
1.の条件の場合は
どちらのスイッチも押されていないと、モータは動かない…
つまり、安全上どちらかのスイッチが切れた場合は
モータを動かしてはいけない… →AND回路
という条件付きでの動作を表すことになります。
2.の条件の場合は
どちらかのスイッチが押されていれば、モータが動く…
つまり、離れた場所にスイッチが存在していて
どちらかが押されれば、動かすことが可能!→OR回路
という形で
遠隔動作にも使用することが可能です。

条件に応じて
これらAND、OR回路を使い分けて
“どういう条件の時に、出力をONするか?“
これを考えることが
ラダープログラムを行う上での
最も大事な要素となります!
これら、AND、ORの積み重ねが
ラダーによるシステム構築の
ほぼ全てを担っているので
今日、この記事を読み終えたあなたは
システムを組むための素養が備わったということになります!

おめでとうございます♪
さぁ、一緒にプログラミングしていきましょう!!
いかがでしたか?
論理回路の重要性と
いかにラダーを組むうえで
論理回路が重要か?
ご理解いただけたかと思います。
そして、この基礎が出来ていれば
ほとんどのラダーを読むことが可能になります!
もちろん、ここから
あなた自身の中で落とし込んでいただかないと
応用していくことは難しいかもしれませんが
沢山失敗して
積み重ねていってみてください!

そうすれば
必ず、点と点でしか理解できなかった部分が
いつか線で繋がってきます!
先ずは、沢山経験して
多くのラダーに触れることで
どんどんあなたの中で理解を深めてみて下さいね♪
そんな中で
どうしても、この回路が理解できない…
この処理の組み方を教えてほしい…
そんな時は
遠慮なく、私にお伝えください!
是非、コメント
もしくは お問い合わせフォームから
ご一報くださいね。
私の持てる知識が
困っている皆さんのためになるのであれば
これ程嬉しいことはありません!!
しっかりと学び、経験して
あなたのものにしていって下さいね!
では、またねー!!
かなとでした♪
※※お問い合わせフォームは、以下から ↓↓↓ ※※





コメント